MotifHub

The recent development in high-throughput chromatin capture technology (e.g. Hi-C) enables us to capture the chromatin-interacting sequence groups on where trans-acting DNA motif groups can be discovered. The problem difficulty lies in the combinatorial nature of DNA sequence pattern matching and its underlying sequence pattern search space. We propose to develop MotifHub for trans-acting DNA motif group discovery on grouped sequences. Specifically, the main approach is to develop probabilistic modeling for capturing the stochastic nature of DNA sequence patterns. Based on the modeling, we develop global sampling techniques to address the global optimization need for model fitting with latent variables. Our results based on expectation maximization and Gibbs sampling demonstrate its solution with linear time complexities.

Downloads

For source codes and potential collaboration, please email here or download here

Command Line Usage

MotifHub maxMotifWidth numOfMotifGroups threshold maxIterations file1 file2 [file3] [file4] ......

Input Arguments:
maxMotifWidth	Maximal motif length in nucletoide (example: 15)
numOfMotifGroups	Number of motif groups (example: 2)
threshold	The tolerance used for testing convergence (example: 0.05)
maxIterations	Maximal number of EM iterations (example: 100)
file1	The first input sequence file path in FASTA format (example: SequenceSet1.fasta)
file2	The second input sequence file path in FASTA format (example: SequenceSet1.fasta)
file3	The third input sequence file path in FASTA format (example: SequenceSet1.fasta)
file4	The forth input sequence file path in FASTA format (example: SequenceSet1.fasta)
......	The other input sequence file paths in FASTA format (example: SequenceSet1.fasta)
Output Files:
All motif group information will be outputted in the MotifHub_results folder.
All motif group images will be outputted in the MotifHub_images folder.
Microsoft Windows 64-bits examples:
C:\> MotifHub <argument_list>
C:\> MotifHub 2 0.05 100 15 SequenceSet1.fasta SequenceSet2.fasta
C:\> MotifHub 2 0.05 100 15 SequenceSet1.fasta SequenceSet2.fasta SequenceSet3.fasta SequenceSet4.fasta
C:\> MotifHub 4 0.1 1000 25 SequenceSet1.fasta SequenceSet2.fasta SequenceSet3.fasta SequenceSet4.fasta
Linux 64-bits examples:
>./run_MotifHub.sh <mcr_directory> <argument_list>
>./run_MotifHub.sh /usr/local/MATLAB/R2017b 2 0.05 100 15 SequenceSet1.fasta SequenceSet2.fasta
>./run_MotifHub.sh /usr/local/MATLAB/R2017b 2 0.05 100 15 SequenceSet1.fasta SequenceSet2.fasta SequenceSet3.fasta SequenceSet4.fasta
>./run_MotifHub.sh /usr/local/MATLAB/R2017b 4 0.1 1000 25 SequenceSet1.fasta SequenceSet2.fasta SequenceSet3.fasta SequenceSet4.fasta

FAQ

What is MotifHub ?

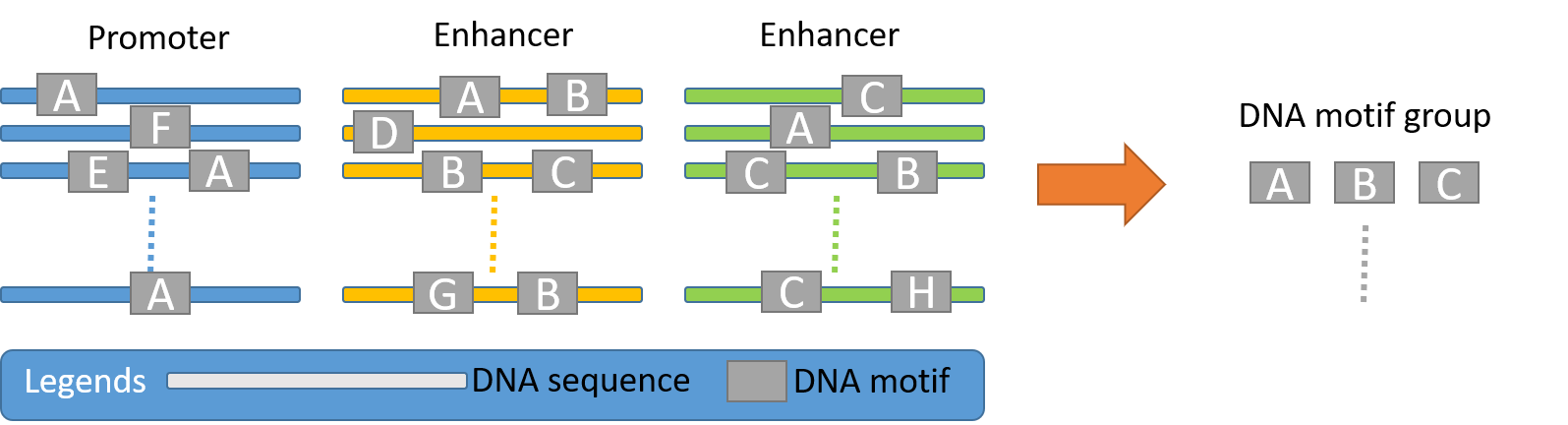
Based on our previous expertise in motif modeling and discovery (pmid30590725, pmid28633280, pmid23814189), we aim at developing probabilistic models for discovering DNA motif groups (e.g. multiple ordered DNA motif patterns) on grouped sequences (e.g. chromatin-interacting promoter-enhancer sequence groups). There are several advantages in choosing probabilistic modeling for this problem. Firstly, DNA motif patterns are known for its degeneracy because of the underlying protein-DNA binding dynamics (pmid16601727). Secondly, the probabilistic nature can enable us to develop models robust to random sequence noises. Thirdly, the combinatorial nature of motif grouping is inherently challenging and should be solved with well-grounded open-box models for biological insights. Generalizing the previous pair setting (pmid28633280), we have derived the mathematical modeling and its fitting algorithms based on expectation maximization and Gibbs sampling. In particular, two versions have been developed, namely MotifHub(EM) and MotifHub(Gibbs). This website harbours MotifHub(Gibbs), given its robust performance.

 

What is MCR ?

MCR stands for Matlab Compiler Runtime. If your machine does not have Matlab, you need to install MCR to execute MotifHub. MCR can be downloaded from the internet easily (e.g. https://www.mathworks.com/products/compiler/matlab-runtime.html). In particular, we advise you to download the same version indicated in the "Downloads" section.

Is there any demo ?

By default, a small testing dataset (SequenceSet1.fasta, SequenceSet2.fasta, SequenceSet3.fasta, SequenceSet4.fasta) is zipped with the MotifHub executables in the "Downloads" section. Once downloaded, you can simply change your current directory to it and type "MotifHub 2 0.05 100 15 SequenceSet1.fasta SequenceSet2.fasta SequenceSet3.fasta SequenceSet4.fasta" to run a MotifHub demo on the testing dataset (which has 2 DNA motif groups to be discovered from the 100 sequence groups of order 4). After the run, you will see the 2 DNA motif groups discovered by MotifHub. Details can be found in the result folders "MotifHub_images" and "MotifHub_results" generated; for instance, the below are the 2 DNA motif groups discovered. (Note: The discovery order may vary. It is normal in de novo motif group discovery as we did not know the discovery order in advance.)

More data ?

Public genome annotation data can be accessed through ENCODE consortium and Gene Expression Omnibus (GEO).

Contact

Please internet-engine-search and contact "Ka-Chun Wong" for any enquiry; for instance, Google Search and Baidu Search.